Generating String Quartets with Neural Networks

Jan 16, 2019

For my final project for Introduction to Neural Networks, my project partner Xiaohan Ding and I put together an ensemble of recurrent neural networks to learn and compose string quartets in the style of Joseph Haydn.

Our initial ambition was set on building long-term structure into music, which at the time seemed to be an elusive problem that a lot of papers pointed out, but none provided any solutions nor insights to tackle it.

We presented our plan to our professor, whose feedback steered us toward something "simpler". Looking back, I wish we had refined and narrowed the problem a bit more - I can spot a ternary form or sonata form when I see one, but what does long-term structure mean? Does it mean that we find ways to inject a prior that makes the computer generate compositions in sonata form? Or that the computer will generate something completely new that contains some (possibly un-classified) underlying structure?

Being a completely newbie, the premise of my goal was not very well-defined. Not know how to get guidance on what we originally wanted to do, we decided to go with the suggestion and try out something simpler instead - simply modeling music with neural networks and see what kind of results we get, aka throw solutions at things until a problem presents itself.

Getting Into It

There were many works in the domain of music generation with machine learning models, each employing ever more complex architectures, such as tied parallel networks by D. Johnson, convolutional generative adversarial networks by Yang et al, and HARMONET by Hild et al.

For our project, we wanted to model music that was more complex than J.S. Bach's chorales, since we thought they were overused. The most natural next step were string quartets because they were similar to the chorales, but instead has a lot more rhythmic and harmonic complexity.

For those who are not familiar with the Western classical music tradition, a string quartet consists of four instruments - two violins, a viola, and a cello. Each instrument occupies a different range, from roughly G6 for the first violin part (yes, yes, violins can go much higher, but rare during the Classical era) to C2, which is the lowest note that can be played on the cello.

Network Architecture

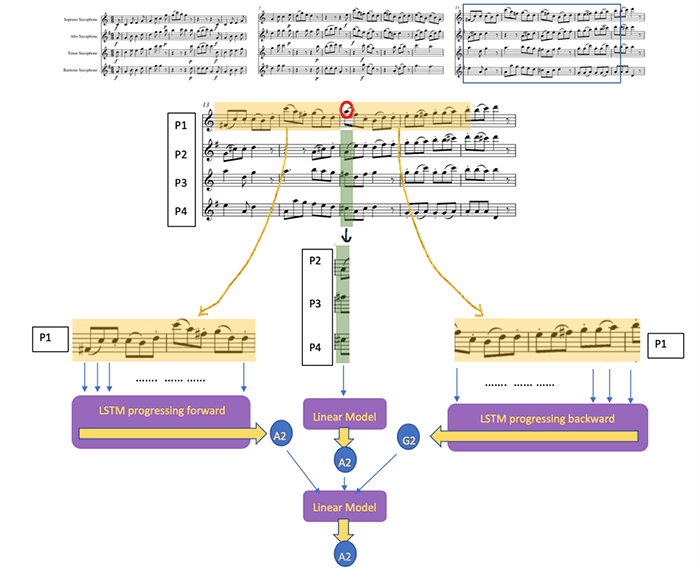
Besides having a larger range than a four-part chorale, string quartets during Haydn's time were also more rhythmically complex. To model such complexity, we employ an ensemble of 16 neural networks, each one modeling one aspect of the music for one of the four instruments. For each instrument, we create a recurrent network to model the forward rhythmic pattern, forward pitch pattern, as well as the backward rhythmic and pitch pattern.

The 16 models alone were not able to capture string quartet well, because we still have not incorporated the element of harmony, which is the sound created by all four instruments being played at the same time. To address this, we added another linear model that looked at the music harmonically at a given moment, and decides what was the most optimal.

Finally, a judge model takes the input from all of the previous models, and outputs a final note that has the least amount of loss.

Architecture of our neural network, which consists of (1) forward pitch model, (2) forward rhythm model, (3) backward pitch model, (4) backward rhythm model for each of the parts. Then we use a linear model to look at the harmony across the four parts, and a final classification model to generate a note.

Data Collection

One thing I learned about myself through this experience was that I never seemed to like to make things easy for myself.

One of the first challenges was the lack of ready-to-use data. The Bach chorales were so popular that they are like the ImageNet of music generation. For Haydn string quartets, I had to get my hands dirty and find them myself.

After poking around, I ended up downloading (more like "farmed") MIDI files from all over the internet to get a good collection. I used the library Music21 to do the preprocessing. Luckily this library provided most of the utilities and abstraction for working with music, such as loading in the MIDI file, separating out the tracks, and providing all of the notations on the music. We also used this library, along with MuseScore to visualize and playback the music the networks come up with later.

Training & Generation

To train the models, we created four-measure frames around each of the notes in the music and supply all but that particular note. The judge model produces a probability distribution over the 88 notes on the piano, and we back-propagate the cross-entropy loss between the predicted distribution and the actual one-hot distribution. Looking back at this a few years later, the training regime is basically the token prediction task used to pre-train language models.

To generate notes, we used a Markov-Chain Monte Carlo (MCMC) sampling approach. We start by generating a random set of notes and rhythm, then iterate through it by first randomly selecting a note, processing its neighborhood with our network to come up with a better replacement. Once we get a replacement, we replace the current note with the generated one. We rinse and repeat until convergence (or rather more realistically, we ran out of time). See the image below for a before vs. after (10000 iterations).

A before and after of the sampling process after 10000 iterations. On the left, we have music that was randomly generated. On the right, we have music that has gone through the sampling process for 10000 iterations.

Results

To complete the project, we created a survey consisted of three short samples generated from our algorithm, as well as three samples from actual composers - somewhat of a musical Turing test. Take a listen below and see if you can tell the difference!

Note that we normalized the music by generating the real ones with computer (as opposed to using live performances).

Discussions

While we did manage to fool a few with untrained ears (who thought the somewhat jazzy #1 was by Haydn), the results were far from realistic.

After a few thousand iterations of sampling and replacement, the harmony at any given 16th note (the smallest unit of time we quantized everything into) made sense. But when you take a step back, the overall music made little sense and sounded more like Schoenberg than Haydn.

We thought this was likely due to the lack of a mechanism to make all four parts coherent in a larger window - the models we employed only look at coherence at the instrument level, as well as coherence across instruments at any given slice of time (i.e. all the 16th notes). This would likely also help to generate some interesting rhythms across all four instruments, rather than all four lines doing their own thing, resulting in the output sounding a a sound soup.

On the bright side though, it did produce some interesting melodic lines, such as around 8th second of Sample #1.

If you are interested in the details, the code repository for this project is here, and we also did a write up of this, which can be found here.